Integrable Quantum Field Theory
“All men are equal, just that some are more equal than others”
-- George Orwell, Animal Farm
Exactly solvable models in (1+1) dimensional quantum field theory and in two-dimensional classical statistical mechanics have a common property, i.e. commuting transfer matrices. The quantum inverse scattering theory (and the Yang-Baxter equation on which is based) has placed the theory of exactly solvable models in a unified framework and has provided a powerful method for studying these models. The Yang-Baxter relation is a sufficient
condition for solvability Moreover, this functional equation leads to a consistent and effective method to find new solvable models: the discovery of an infinite number of solvable lattice models in the last twenty years was indeed accomplished in this way. These models exhibit independent critical behavior and are expected to exhaust an important set of universality classes in two dimensions.
Conformal field theory has given strong support to this conjecture, opening at the same time a remarkable new perspective on an infinite class of novel quantum field theories with extended symmetries and, correspondingly, on the possible behavior of matter in two dimensional systems.
Many massive deformations of the conformal models fall also elegantly in the class of integrable models and their solution has been obtained in terms of elastic scattering S-matrix theory: as shown by A.B. Zamolodchikov, one of the long-standing problems of
statistical mechanics, i.e. the solution of the Ising model in a magnetic field (at the critical temperature) admits in fact an exact solution in terms of an elastic S-matrix that involves eight massive particles in bootstrap interaction. This solution shows a deep relation with the algebraic structure encoded in the Dynkin diagram of the exceptional algebra. The exact computation of the spin-spin correlation function of this model has been done in a paper with G. Delfino by using integrability and Form Factors and successfully checked against both numerical simulations and experiments of neutron scattering in quantum spin chains.
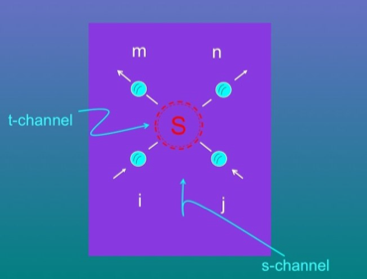
Two-body S-matrix
The key idea behind integrable quantum field theories is about the self-consistent dynamical method for computing the exact expressions of all scattering amplitudes and the mass of the quasi-particle excitations. This goes under the name of bootstrap appraoch, where all particles are democratically on the same footing: there is no distinction between particles of the asymptotic states and those of the bound states, and any massive excitation of the theory can equivalently be regarded as asymptotica state or a bound state of a pair of particles of the same theory.
The bootstrap approach has deeply changed our way to look at the dynamics of two-dimensional statistical models. Thanks to S-matrix theory, one can even find exact solution of non-unitary models, as shown for the case of Yang-Lee edge singularity. Elegant connection to exceptional algebras, like E8, E7 and E6, has been found for the Ising model, the Tricritical Ising model and the 3-state Potts model. Moreover, it can be also extended to massless field theories associated to Renormalization Group flow between two fixed point.
Massless Renormalization Group Flows
It is worth remind that the paradigmatical integrable quantum field theory, namely the Sine-Gordon model, has found innumerable applications to condensed matter and statistical problems.
Main References
A.B. Zamolodchikov and A.B. Zamolodchikov, Factorized S-matrices in two dimensions as the exact solutions of certain relativistic quantum field theories, Ann. Phys. 120 (1979), 253.
A.B. Zamolodchikov, Integrable field theory from conformal field theory, Adv. Stud. Pure Math. 19 (1989), 641.
• G. Mussardo, Statistical Field Theory. An Introduction to Exactly Solved Models of Statistical Physics, Oxford University Press 2010.
G. Mussardo, Off-critical statistical models: factorized scattering theories and bootstrap program, Phys. Rep. 218 (1992) 215 .
• F.A. Smirnov, Reductions of the Sine-Gordon model as perturbation of minimal models of conformal field theory, Nucl. Phys. B 337 (1990), 156.
F.A. Smirnov, Exact S-matrices for Phi12 perturbed minimal models of conformal field theory, Int. J. Mod. Phys. A6 (1991), 1407.
R. Coldea, D.A. Tennant, E.M. Wheeler, E. Wawrzynska, D. Prabhakaran, M. Telling, K. Habicht, P. Smeibidi, K. Kiefer, Quantum Criticality in an Ising Chain: Experimental Evidence for Emergent E(8) Symmetry, Science 327:177-180, 2010.
G. Mussardo, P. Christe, Integrable Systems away from Criticality: the Toda Field Theory and the S-matrix of the Tricritical Ising Model, Nucl. Phys. B 330 (1990), 465-487
J.L. Cardy, G. Mussardo, S-matrix of the Yang-Lee Edge Singularity in Two Dimensions, Phys.Lett.B225 (1989), 275-278
H.W. Braden, E. Corrigan, P.E. Dorey, R. Sasaki, Affine Toda Field Theory and exact S-matrices, Nucl. Phys. B 338 (1990), 689.
V. A. Fateev, A. B. Zamolodchikov, Conformal field theory and purely elastic S-matrices, Int. J. Mod. Phys. A 5 (1990), 1025.
A.B. Zamolodchikov, Al. B. Zamolodchikov, Massless factorized scattering and sigma models with topological term, Nucl.Phys.B379:602-623,1992.
Some Other Relevant Publications
G. Mussardo, S. Penati, A Quantum field theory with infinite resonance, Nucl. Phys. B 567:454-492,2000. hep-th/9907039
G. Mussardo, P. Simon, Bosonic type S matrix, vacuum instability and CDD ambiguities, Nucl.Phys.B578:527-551,2000, hep-th/9903072
A. De Martino, M. Moriconi, G. Mussardo, Reflection Scattering Matrix of the Ising Model in a Random Boundary Magnetic Field, Nucl. Phys. B 509 (1998) 615-636
A. LeClair, A. Ludwig, G. Mussardo, Integrability of coupled conformal field theories, Nucl.Phys.B512:523-542,1998, hep-th/9707159
D. Cabra, A. Honecker, G. Mussardo, P. Pujol, A non-perturbative approach to the random bond Ising model, J. Phs. A 30 8415-8426, 1997, hep-th/9705180.
G. Mussardo, P. Simonetti, Random bond Ising model and massless phase of the Gross-Neveu model, Phys.Lett.B351:515-518,1995, hep-th/9503011
G. Mussardo, Integrable deformations of the nonunitary minimal conformal model M(3,5), Int.J.Mod.Phys.A7:5027-5044,1992.
F. Colomo, A. Koubek, G. Mussardo, On the S matrix of the subleading magnetic deformation of the tricritical Ising model in two-dimensions, Int.J.Mod.Phys.A7:5281-5306,1992, hep-th/9108024
A. Koubek, M.J. Martins, G. Mussardo, Scattering matrices for Phi(1,2) perturbed conformal minimal models in absence of kink states, Nucl.Phys.B368:591-610,1992.
A. Koubek, G. Mussardo, Phi(1,2) deformation of the M(2,2n+1) conformal minimal models, Phys.Lett.B266:363-369,1991.
[M. Koca, G. Mussardo, Mass Formulae in Toda Field Theories, Int. Journ. Mod. Phys. A6 (1991), 1543-1565.
A. Koubek, G. Mussardo, R. Tateo, Bootstrap trees and consistent S matrices, Int. J. Mod. Phys. A7:3435-3446,1992